GAMS supports the teaching and application of optimization within academic institutions.
We provide complimentary access to GAMS through our community and course licenses in order
to offer professors and students the best options to teach and learn about optimization.
Request a complimentary, time-limited, and fully featured GAMS license that enables
you to evaluate and explore the different solvers from our portfolio
before making a purchasing decision.
VIOOH is a leading global digital out of home (OOH) marketplace. Launched in 2018 and with headquarters in London, VIOOH’s platform connects buyers and sellers in a premium marketplace, making OOH easily accessible.
VIOOH is a leading out of home advertising expert
Led by a team of digital OOH and programmatic tech experts, VIOOH is pioneering the transformation of the OOH sector, championing its role in enhancing omni-channel digital campaigns through the use of programmatic capabilities and data. VIOOH currently trades programmatically in 15 markets, with more to follow.
Problem
VIOOH empowers media owners in the construction of Out of Home marketing campaigns for their clients. Media owners own a large inventory of advertising panels which they want to efficiently manage while satisfying as much as possible the business requirements of their clients.
Put simply, the problem to solve is matching a subset of traditional “static” and/or digital panels (inventory) for each new incoming campaign that satisfies the requirements.
The optimum panel allocation is the problem to solve
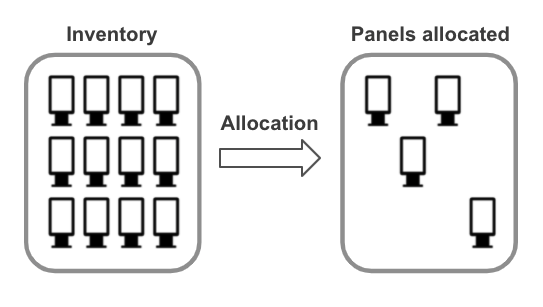
We can see this as a combinatorial problem in mathematics. There are many combinations of panels but we want a selection that best fits the business objectives. Yet it can be very complex to satisfy all the objectives.
For instance, a typical list of requirements could be:
Campaign broadcast on 100 panels
Campaign seen by at least 2M people
Maximal budget: £100K
Geographical repartition:
50% of the panels in London
30% in Manchester
20% in Bristol
Proximity targeting: at least 80% of the panels in a radius of 500 meters to a fast food restaurant
Maximize impacts on the 24-34 years old population
In order to tackle these requirements, the problem is expressed as an optimization program. The requirements are defined either as objectives to maximize or constraints to obey. As media owners continuously simulate campaigns and expect a solution in a few seconds, speed is one of our main challenges.
Optimization Program
Objectives
The objectives can either be explicit or implicit in nature.
Explicit objectives are the quantities expressed by the media owners or their clients. For instance, the number of panels is a quantity that we try to reach as close as possible. These quantities are measurable, we can easily assess the quality of the results.
The implicit objectives on the other hand do not have quantifiable targets. For example, geographical spread is one of them. We try to spread the panels across a territory as much as possible.
Constraints
There are two types of constraints:
Some are “soft” constraints, i.e. it is allowed to violate them to avoid infeasibility issues, and the media owner will evaluate the solution and decide whether or not to accept it.
“Hard” constraints must be respected. For instance, in out-of-home advertising there are very strict prohibitions rules. One example of this is no alcohol advertising next to a school. Another is that we cannot have two competing clients on the same panel (digital panels typically host up to 6 advertisers within the same 1 hour slot, on a rotational basis). These constraints are of higher priority than any objectives. The objectives might be degraded to fulfill them.
At a glance, the program is composed of 23 sets, 46 parameters, 18 blocks of variables and 29 blocks of equations. The size of each problem depends on the inventory of the media owner and the number of campaigns to allocate.
The VIOOH Tech Stack
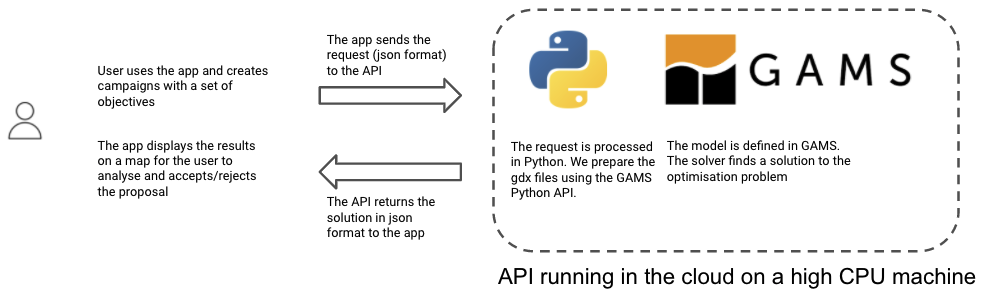
The VIOOH platform is composed of microservices. The UI and the backend application is in a common language (Javascript & Java). The optimization program is encapsulated in a Python API. The API receives all the campaign data (duration, eligible inventory, etc.) from the front-end application in a JSON format. The data preparation and creation of the GDX files are performed using the GAMS Python API. The optimization program is written in a GAMS file
The optimization solution is implemented as a GAMS model and communicates with the custom frontend
Conclusion
A simpler approach could have been to use a “greedy algorithm” to solve the allocation problem. This style of approach would mean that not every possible solution is evaluated but rather a seemingly good solution can be found by ranking panels against the objectives and then choosing them one by one according to that order. However, as the complexity of campaigns has increased over time and continues to do so, it is not possible for this style of algorithm to balance all of the objectives and still find quality solutions in all cases. Using an optimization program is a real game changer and with this VIOOH are able to solve very complex marketing needs in a timely manner.
About VIOOH
VIOOH is a leading global digital out of home (OOH) marketplace. Launched in 2018 and with headquarters in London, VIOOH’s platform connects buyers and sellers in a premium marketplace, making OOH easily accessible.
